SQL Queries

The following examples are not mine but this is soooo cool :)

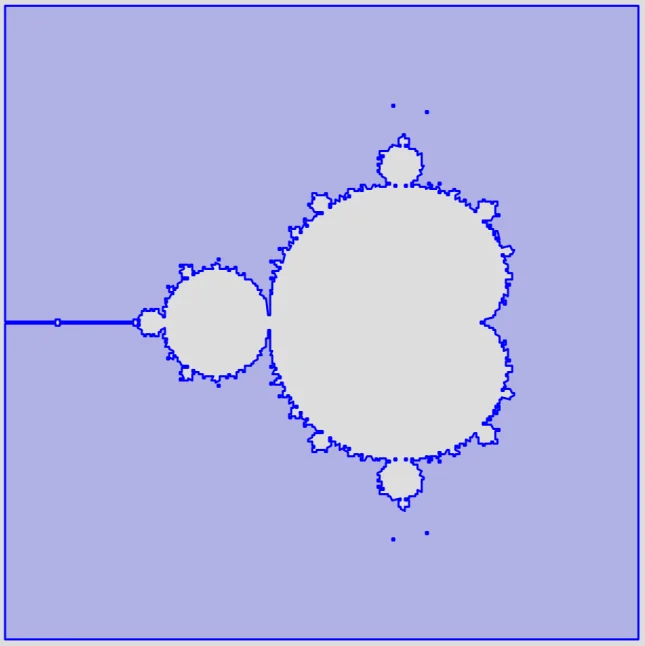
Mandelbrot Set

Source: https://blog.jooq.org/fun-with-postgis-mandelbrot-set-game-of-life-and-more/

With the code below, use different values for "dims" to zoom in, e.g.

dims (r1, r2, i1, i2, s, it, p) as (values (
  (-0.925-0.032)::float, (-0.925+0.032)::float, 
  (0.266-0.032)::float, (0.266+0.032)::float, 
  0.00005::float, 100, 256.0::float)
)

Code

WITH RECURSIVE

  -- These are the dimensions that you can play around with
  dims (r1, r2, i1, i2, s, it, p) AS (
    VALUES (

      -- The dimensions of the real axis
      -2::float, 1::float, 

      -- The dimensions of the imaginary axis
      -1.5::float, 1.5::float, 

      -- The step size on each axis, per pixel or sprite
      0.01::float, 

      -- The maximum number of iterations
      100, 

      -- "Infinity", i.e. when to stop
      256.0::float
    )
  ),

  -- The square again, as before
  sprites (s) AS (VALUES
    (st_polygonfromtext('polygon ((0 0, 0 1, 1 1, 1 0, 0 0))'))
  ),

  -- The number plane, as ints
  n1 (r, i) AS (
    SELECT r, i 
    FROM
      dims, 
      generate_series((r1 / s)::int, (r2 / s)::int) r,
      generate_series((i1 / s)::int, (i2 / s)::int) i
  ),

  -- The number plane as scaled floats
  n2 (r, i) AS (
    SELECT r::float * s::float, i::float * s::float
    FROM dims, n1
  ),

  -- The recursive calculation of the Mandelbrot formula
  -- zn = (zn-1)^2 + c
  l (cr, ci, zr, zi, g, it, p) AS (
    SELECT r, i, 0::float, 0::float, 0, it, p FROM n2, dims
    UNION ALL
    SELECT cr, ci, zr*zr - zi*zi + cr, 2*zr*zi + ci, g + 1, it, p 
    FROM l

    -- The recursions stops when we reach the maximum
    WHERE g < it

    -- Or, when we reach "infinity"
    AND zr*zr + zi*zi < p
  ),

  -- Find the last calculated value per point in the
  -- complex number plane c (cr, ci), discard the others
  x (cr, ci, zr, zi, g) AS (
    SELECT DISTINCT ON (cr, ci) cr, ci, zr, zi, g
    FROM l
    ORDER BY cr, ci, g DESC
  )

-- Turn every calculated point into a square
SELECT
  st_union(
    st_translate(sprites.s, round(cr / dims.s), round(ci / dims.s))
  )
FROM x, sprites, dims

-- Retain only the points *not* belonging to the Mandelbrot set
-- You can also inverse the equation to retain the points that
-- belong to the set
WHERE zr*zr + zi*zi > p;

Example output:

mandelbrot

Another mandlebrot alternative

WITH RECURSIVE  xaxis(x) AS (VALUES(-2.0) UNION ALL SELECT x+0.05 FROM xaxis WHERE x<1.2),
  yaxis(y) AS (VALUES(-1.0) UNION ALL SELECT y+0.1 FROM yaxis WHERE y<1.0),
  m(iter, cx, cy, x, y) AS (
    SELECT 0, x, y, 0.0, 0.0 FROM xaxis, yaxis
    UNION ALL
    SELECT iter+1, cx, cy, x*x-y*y + cx, 2.0*x*y + cy FROM m 
     WHERE (x*x + y*y) < 4.0 AND iter<28
  ),
  m2(iter, cx, cy) AS (
    SELECT max(iter), cx, cy FROM m GROUP BY cx, cy
  ),
  a(t) AS (
    SELECT group_concat( substr(' .+*#', 1+min(iter/7,4), 1), '') 
    FROM m2 GROUP BY cy
  )
SELECT group_concat(rtrim(t),x'0a') as Mandelbrot FROM a;

Example output:

mandelbrot

Christmas Tree

ASCII art christmas tree using Recursion and CTEs.

Source: https://learnsql.com/blog/draw-christmas-tree-sql/

Code

WITH small_tree(tree_depth,pine) AS (
  SELECT 1 tree_depth,
  rpad(' ',10,' ') || '*'
  || rpad(' ',20,' ') || '*'
  || rpad(' ',20,' ') || '*'
  pine
  FROM   dual
  UNION ALL
  SELECT small_tree.tree_depth +1 tree_depth,
  rpad(' ',10-small_tree.tree_depth,' ') || rpad('*',small_tree.tree_depth+1,'.') || lpad('*',small_tree.tree_depth,'.')
  || rpad(' ',20-small_tree.tree_depth-tree_depth,' ') || rpad('*',small_tree.tree_depth+1,'.') || lpad('*',small_tree.tree_depth,'.')
  || rpad(' ',20-small_tree.tree_depth-tree_depth,' ') || rpad('*',small_tree.tree_depth+1,'.') || lpad('*',small_tree.tree_depth,'.') pine
  FROM   small_tree
  where small_tree.tree_depth < 10
)
SELECT pine
FROM small_tree;

Result

          *                    *                    *
          *.*                  *.*                  *.*
        *...*                *...*                *...*
        *.....*              *.....*              *.....*
      *.......*            *.......*            *.......*
      *.........*          *.........*          *.........*
    *...........*        *...........*        *...........*
    *.............*      *.............*      *.............*
  *...............*    *...............*    *...............*
  *.................*  *.................*  *.................*

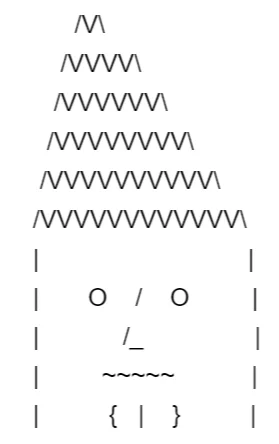
Man with a Hat

Draw a man with a hat using recursive queries and Common Table Expressions (CTEs).

Source: https://learnsql.com/blog/draw-sql-recursive-queries/

Code

WITH RECURSIVE hat
AS (
  SELECT
    CAST(REPEAT(' ', 11) || '/V\' AS VARCHAR(100))
      AS hat_pattern,
    1 AS level

  UNION ALL

  SELECT
    CAST(
      REPEAT(' ', 10-level) || '/'
        || REPEAT('V', 2 * level + 1) || 'V\'
        AS VARCHAR(100))
      AS repeated_pattern,
    hat.level + 1
  FROM hat
  WHERE level < 6
)


SELECT hat_pattern
FROM hat

UNION ALL

SELECT
  CAST(
    REPEAT(' ', 5) || '|' || '             ' || '|'
    AS VARCHAR(100))
  AS forehead

UNION ALL

SELECT
  CAST(
    REPEAT(' ', 5) || '|' || '  O   /   O  ' || '|'
    AS VARCHAR(100))
  AS eyes

UNION ALL

SELECT
  CAST(
    REPEAT(' ', 5) || '|' || '     /_      ' || '|'
    AS VARCHAR(100))
  AS nose

UNION ALL
SELECT
  CAST(
    REPEAT(' ', 5) || '|' || '     ~~~~~   ' || '|'
    AS VARCHAR(100))
  AS mouth

UNION ALL
SELECT
  CAST(
    REPEAT(' ', 5) || '|' || '   {  |  }   ' || '|'
    AS VARCHAR(100))
  AS chin;

sql-hat-guy